What if someone tells you that the entire existing security protocols of the internet can be broken by proving a mathematical equation? A clever person like you will say: It can be or it can’t be but who knows until someone proves the equation? Yes, you are right. You don’t know if the problem can ever be solved. But, if someone solves the problem then you can talk about its impact.
There are many such problems in this world which are hard to solve but once you solve them, it’s easy to verify the solution. The problems which are non-deterministic and the problems which are undecidable. Simply, the problems that we would love to solve but are unable to do so exactly.
In mathematics, there are several complexity classes for the problems. If you can solve a problem in polynomial time (we can predict the maximum amount of time it will take to solve the problem), such problem will be called ‘P-class‘ problem. But, if you are not sure about the solution in polynomial time, such problem will be called ‘NP-class‘ problem. P class is the set of problems that can be solved in polynomial time. NP is the set of problems whose solutions can not be determined but can be verified in polynomial time.
Here, the first two paragraphs are about NP-class problems.
Ok, I know that you are reading this article to know about that magical equation which, once proved, can break all the existing security protocols of the internet. In fact, the Clay Institute is offering one million dollars for a solution to the problem. So let’s talk about the equation which I considered you might be interested in.
Is P=NP?
Yes, two operands and an operator. Is ‘P class problem‘ equals to ‘NP-class problem‘? Well, this is the major unsolved problem in computer science. It asks whether every problem whose solution can be quickly verified by a computer can also be quickly solved by a computer? According to the definitions we discussed:
- A yes-or-no problem is in P class if the answer can be computed in polynomial time.
- A yes-or-no problem is in NP class if a yes answer can be verified in polynomial time.
Now we can say that if a problem is in P class, then it is in NP class also. Because for any problem inP, we can verify the answer by simply recalculating the answer. Now, the question is, whether all problems in NP are in P?. Does the fact that we can verify an answer in polynomial time mean that we can compute that answer in polynomial time?
There are large number of important problems which is known to be NP-complete (basically, if any of these problems are proven to be in P, then all NP problems are proven to be in P). If P = NP, then all of these problems will be proven to have an efficient (polynomial time) solution.
It is one of the seven Millennium Prize Problems selected by the Clay Mathematics Institute to carry a US$1,000,000 prize for the first correct solution.
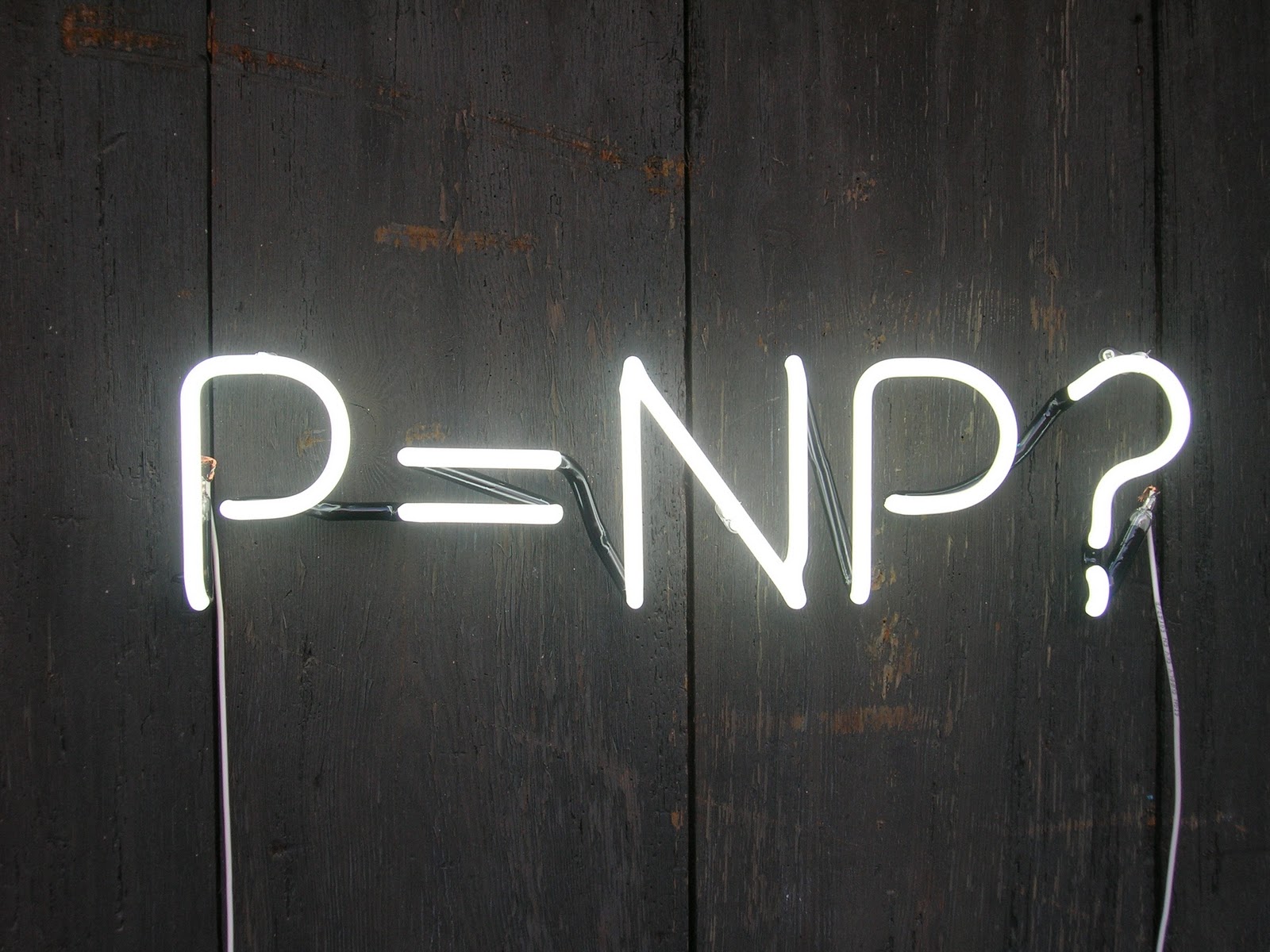
No comments:
Post a Comment